Historie Gauss-Krügerova zobrazení
Gauss-Krügerovo přímé konformní zobrazení elipsoidu do roviny = t r a n s v e r z á l n í v á l c o v é zobrazení v poledníkových pásech, kde se válce dotýkají zemského elipsoidu podél předem zvolených určitých meridiánů, které se pak zobrazují nezkresleně do roviny jako osy souřadnic x.
Zajímavá je historie tohoto zobrazení. První válcová zobrazení (čtvercová mapa Marinova a Mercartorovo zobrazení) byla omezena na zobrazení zemské koule a použití zeměpisných souřadnic (délek a šířek). Původcem tranzversálních zobrazení je francouzský geodet Cassini, který v r. 1734 užil poprvé pravoúhlých souřadnic (kde meridián nahrazuje rovník) a na krátké vzdálenosti je užíval jako pravoúhlých rovinných souřadnic. Podnítil tím Clairauta k rovnici pro geodetickou křivku. Roku 1809 použil Soldner pravoúhlých souřadnic pro zobrazení Bavor (Bayern) v pásu 350 km širokém, a od té doby se rozšířil tento způsob nejen v Německu, ale i bývalém Rakousko-Uhersku, kde ho známe pod označením Cassini–Soldnerovo zobrazení. Dodnes používáme platné katastrální mapy, jež jsou zobrazeny ve dvou meridiánových pásech tohoto zobrazení (s počátkem v trigonometru Gusterberg a Sv. Štěpán). Pravoúhlé geodetické souřadnice se převádějí do roviny v původní délce, jakou mají na elipsoidu. Základní meridián se tudíž nezkresluje a jeho blízké okolí je věrně zobrazeno. Ve větších vzdálenostech však dochází k velkým úhlovým zkreslením. Spolu s nepříjemnou vlastností, že délkové zkreslení závisí na směru, je toto zobrazení nevýhodné.
Pro nepříznivé vlastnosti Cassini-Soldnerova
zobrazení se v první polovině 20. století začíná užívat souřadnic konformních,
tzv. Gaussových, kde není směrového zkreslení. Otcem všeobecně platné teorie
konformního zobrazení je geniální německý matematik C. Fridrich G a u s s, který
ji v roce 1825 uveřejnil v díle "Allgemeine Auf1ösung der Aufgabe, die Teile
einer gegebenen Fläche so abzubilden, dass die Abbildung dem Abgebildeten in den
kleinsten Teilen ähn1ich ist". Z názvu díla je již zřejmé, že při konformním
zobrazení je geometrický vztah mezi oběma plochami definován tak, že každému
bodu první plochy odpovídá příslušný bod na druhé ploše a že obraz se podobá v
nejmenších částech svému originálu. Podle své všeobecné teorie vypracoval a
provedl Gauss konformní zobrazení Hannoverska v meridiánovém pásu v letech 1821
– 1825. Bylo to poprvé, kdy se užilo konformních souřadnic v
trigonometrické síti. Triangulace napřed sloužila stupňovému měření, ale pak
byla rozšířena na celé království a dokončena v roce 1844. Pracovalo se podle
tradice a šablon předaných Gaussem; nesmrtelný autor neměl čas uveřejnit
základy svého zobrazení. Po jeho smrti v roce 1855 nikdo neznal teoretický
základ metody, teprve jiný znamenitý německý geodet S c h r e i b e r
podle určitých náznaků v objevených Gaussových dopisech usoudil na jeho metodu,
tuto znovu samostatně vytvořil a uveřejnil v roce 1866 v díle "Theorie der
Projectionsmethode der Hannoverschen La.ndesvermessung" .
Mezitím připadl Hannover k Prusku (Preussen) a bylo pomyšleno na použití Gaussových souřadnic pro katastrální měření. Bohužel, v Prusku se nakonec ujala myšlenka souřadnice rozdělit na 31 souřadnicových soustav podle politického rozdělení státu na kraje; do nich byly také výsledky přepočteny. Těchto 31 konformních soustav bylo roku 1879 opět zrušeno a nahrazeno všeobecně zavedenými Soldnerovými souřadnicemi, nevyjímaje ani Hannoverska.
Roku 1899 pokrylo Preussische Landesaufnahme 400 000 km2 trigonometrickou sítí I. řádu, tedy téměř celé území Německa, vyjma krajů Bayern, Sachsen, Würtenberg, Baden, Mecklenburg a Hohenzollern. Generál Schreiber použil zde Gaussových souřadnic: zobrazil však napřed elipsoid konformně na kouli (podle Gaussových "Untersuchungen liber Gegenstande der höheren Geodäsie" a teprve z koule určil rovinné konformní (Gaussovy) souřadnice. Zvolena byla jediná souřadnicová soustava s hlavním (nezkresleným) meridiánem 31°, pořadnice y dosáhla na západě 540 km a na východě až 622 km. Deformace délkové i směrové byly dosti značné – až 4,6 m na 1 km (4,6 mm na 1 m, takže v triangulaci se musely zavádět opravy i při měření centračních prvků). Tato soustava s tak velikými deformacemi přirozeně nemohla být použita pro katastrální mapování a proto byla pro účely katastru použita jen v úzkém pruhu podél meridiánu 31°.
Dědictvím po jinak znamenitých geodetech 19. století bylo 50 různých souřadnicových soustav na území bývalého Pruska. Tento neudržitelný stav vedl přirozeně ke snaze sjednotit veškeré dosavadní výsledky měření a zavést jednotné konformní souřadnice pro celý stát a všechny druhy map. Rozsah státu nedovolil zvolit tyto souřadnice v jediné soustavě, poněvadž by z toho vyplynuly příliš velké deformace – i při obecné poloze sečného válce by činily až 100 cm na 1 km – a bylo nutno se rozhodnout pro více soustav. Prof. Dr. L. K r ü g e r pro tento účel v díle "Konforme Abbildung des Erdellipsoids in der Ebene", Potsdam 1912, znovu uvedl Gaussovu hannoverskou metodu, kterou počtářsky propracoval pro zobrazení meridiánových pásů 3° širokých ("Fonneln zur Konfonnen Abbildung des Erdellipsoids in der Ebene", Berlin 1919). Roku 1917 došlo k dohodě Německa s bývalým Rakousko–Uherskem o zavedení jednotných společných rovinných souřadnic Gaussových. V roce 1922 se zeměměřičská rada usnesla (der Beirat für das Vermessungswesen) definitivně zavést pro všechny druhy map toto zobrazení v poledníkových pásech 3° širokých, přičemž na okrajích pásů v překrytu 1° širokém (půl stupně na každou stranu) bude nutno počítat souřadnice v soustavách obou pásů. Jako hlavní poledníky (Hauptmeridianen) byly určeny 6., 9., 12., 15., 18., 21. a 24. poledník východně od Greenwiche.
Teorie zobrazení
Podkladem pro zobrazení je všeobecná teorie konformního zobrazení. Každou plochu lze rozdělit na nekonečně malé čtverce dvěma osnovami čar pod pravým úhlem se protínajících (tzv. izotermická síť); pro naše účely je žádoucí, aby aspoň jedna osnova byla složena z geodetických křivek. Ztotožníme-li isotermické sítě na dvou plochách, obdržíme jejich konformní zobrazení. Na kouli můžeme vést nekonečně mnoho takových sítí (jsou to poledníky a. rovnoběžky k libovolně volenému pólu) a proto můžeme kouli zobrazovat do roviny v obecné poloze, na zemském elipsoidu lze vést jen jednu takovou síť poledníků a rovnoběžek a můžeme proto zobrazovat jen v normální poloze. Zvolíme-li v rovině dvě osnovy přímek, což charakterizuje válcové zobrazení, (u kuželového zobrazení volíme svazek paprsků a soustředných kružnic), rozdělili jsme rovinu na nekonečně malé čtverce o stranách dx, dy. Na elipsoidu jim odpovídají elementy M . df a N . cos f . dl, kde f a l jsou zeměpisná šířka a délka. M a N jsou poloměry podélné a příčné křivosti. V rovině a na elipsoidu jsou délkové elementy vyjádřeny:
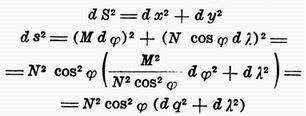
|
Poslední úpravou jsme obdrželi tzv. symetrické souřadnice l a |
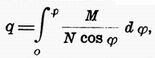 |
jež dávají isotermickou síť na elipsoidu, odpovídající čtvercové síti v rovině. Obecný tvar je dán výrazem ds2 = K2 (dx2 + dy2), kde K je funkcí jedné nebo obou symetrických souřadnic a udává nám hustotu sítě. Poměr délkových elementů v rovině a na elipsoidu čili délkové zkreslení je dáno vztahem:
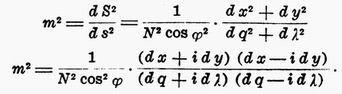
Poloha zobrazovacího pásu na elipsoidu.
Zobrazení pásů v rovině.